odeint

mipylib.numeric.integrate.odeint(func, y0, t, args=())

Integrate a system of ordinary differential equations.

Parameters:

• func – (callable(y, t, …) ) Computes the derivative of y at t.

• y0 – (array) Initial condition on y (can be a vector).

• t – (array) A sequence of time points for which to solve for y. The initial value point should be the first element of this sequence.

• args – (tuple) Extra arguments to pass to function.

Returns:

Array containing the value of y for each desired time in t.

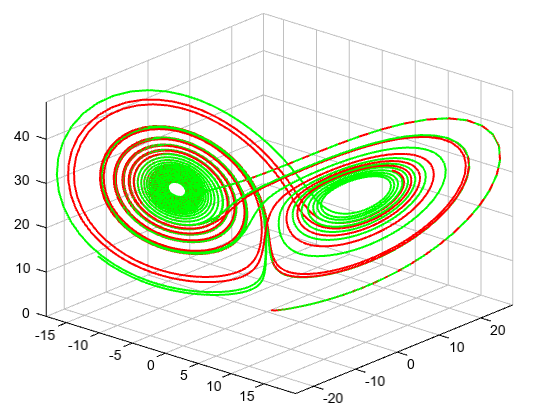
The second order differential equation for the angle theta of a pendulum acted on by gravity with friction.

from mipylib.numeric.integrate import odeint

def pend(y, t, b, c):
    theta, omega = y
    dydt = [omega, -b*omega - c*np.sin(theta)]
    return dydt

b = 0.25
c = 5.0
y0 = [pi - 0.1, 0.0]
t = linspace(0, 10, 101)
sol = odeint(pend, y0, t, args=(b, c))

plot(t, sol[:, 0], 'b', label='theta(t)', linewidth=2)
plot(t, sol[:, 1], 'g', label='omega(t)', linewidth=2)
legend(loc='lower right')
xlabel('t')
grid()

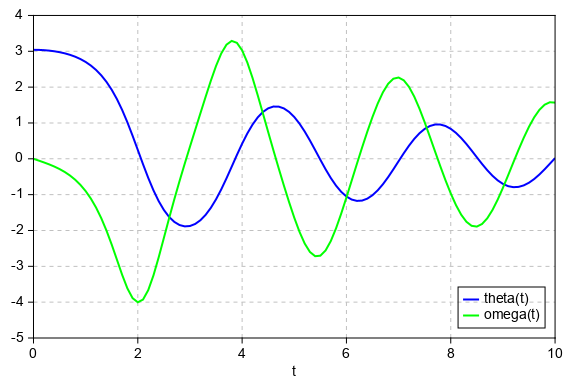
Lorentz absorber.

from mipylib.numeric import integrate

def lorenz(p,t,s,r,b):
    x,y,z = p
    return s*(y-x), x*(r-z)-y, x*y-b*z   # dx/dt,dy/dt,dz/dt

t = np.arange(0, 30, 0.01)
track1 = integrate.odeint(lorenz, (0.0,1.00,0.0), t, args=(10.0,28.0,2.6))
track2 = integrate.odeint(lorenz, (0.0,1.01,0.0), t, args=(10.0,28.0,2.6))

axes3d()
plot3(track1[:,0], track1[:,1], track1[:,2], linewidth=2, color='r')
plot3(track2[:,0], track2[:,1], track2[:,2], linewidth=2, color='g')