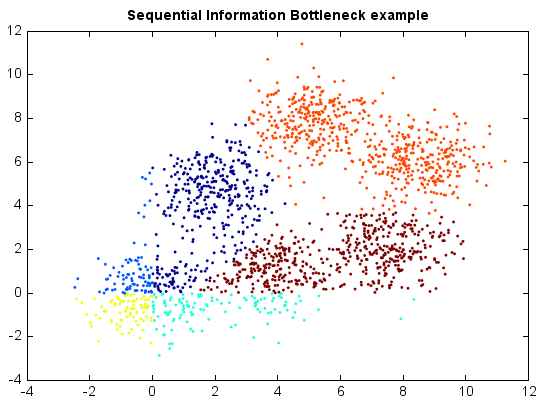
Sequential Information Bottleneck¶
The Sequential Information Bottleneck (SIB) algorithm clusters co-occurrence data such as text documents vs words. SIB is guaranteed to converge to a local maximum of the information. Moreover, the time and space complexity are significantly improved in contrast to the agglomerative IB algorithm.
In analogy to K-Means, SIB’s update formulas are essentially same as the EM algorithm for estimating finite Gaussian mixture model by replacing regular Euclidean distance with Kullback-Leibler divergence, which is clearly a better dissimilarity measure for co-occurrence data. However, the common batch updating rule (assigning all instances to nearest centroids and then updating centroids) of K-Means won’t work in SIB, which has to work in a sequential way (reassigning (if better) each instance then immediately update related centroids). It might be because K-L divergence is very sensitive and the centroids may be significantly changed in each iteration in batch updating rule.
Note that this implementation has a little difference from the original paper, in which a weighted Jensen-Shannon divergence is employed as a criterion to assign a randomly-picked sample to a different cluster. However, this doesn’t work well in some cases as we experienced probably because the weighted JS divergence gives too much weight to clusters which is much larger than a single sample. In this implementation, we instead use the regular/unweighted Jensen-Shannon divergence.
from miml import datasets
from miml.cluster import SIB
fn = os.path.join(datasets.get_data_home(), 'clustering', 'gaussian',
'six.txt')
df = DataFrame.read_table(fn, header=None, names=['x1','x2'],
format='%2f')
x = df.values
model = SIB(k=6, max_iter=100, runs=20)
y = model.fit_predict(x)
scatter(x[:,0], x[:,1], c=y, edgecolor=None, s=3)
title('Sequential Information Bottleneck example')