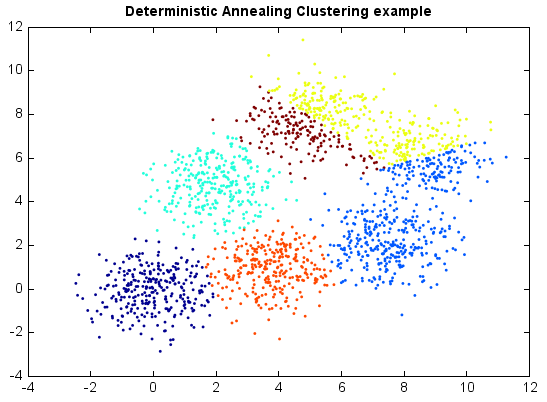
Deterministic Annealing Clustering

The observation of annealing processes in physical chemistry motivated the use of similar concepts to avoid local minima of the optimization cost. Certain chemical systems can be driven to their low-energy states by annealing, which is a gradual reduction of temperature, spending a long time at the vicinity of the phase transition points. In the corresponding probabilistic framework, a Gibbs distribution is defined over the set of all possible configurations which assigns higher probability to configurations of lower energy. This distribution is parameterized by the temperature, and as the temperature is lowered it becomes more discriminating (concentrating most of the probability in a smaller subset of low-energy configurations). At the limit of low temperature it assigns nonzero probability only to global minimum configurations.

from miml import datasets
from miml.cluster import DeterministicAnnealing

fn = os.path.join(datasets.get_data_home(), 'clustering', 'gaussian',
    'six.txt')
df = DataFrame.read_table(fn, header=None, names=['x1','x2'],
    format='%2f')
x = df.values

model = DeterministicAnnealing(12, 0.9)
y = model.fit_predict(x)

scatter(x[:,0], x[:,1], c=y, edgecolor=None, s=3)
title('Deterministic Annealing Clustering example')

#Problem: not consistent with Scala result